Objetivo: Conocer las técnicas de recolección, tabulación, clasificación y codificación de la información cualitativa (atributo) y cuantitativa (variable), a través de la observación y procesamiento de los datos estadísticos.
1. Realizar una presentación donde exprese de manera creativa:
a. Ingresar al DANE y Describir sus funciones

El Departamento Administrativo Nacional de Estadística, o por su sigla DANE, es la entidad responsable de la planeación, levantamiento, procesamiento, análisis y difusión de las estadísticas oficiales de Colombia. Pertenece a la Rama Ejecutiva del Estado Colombiano, con más de 50 años de experiencia.
El DANE ofrece al país y al mundo más de 30 investigaciones de todos los sectores de la economía, industria, población, sector agropecuario y calidad de vida, entre otras. Toda esta labor, sumada a la aplicación de modernas tecnologías de captura, procesamiento y difusión, así como la calidad humana de todos los que participan en el proceso de la organización, permiten al DANE fortalecer el conocimiento, la confianza y la cultura estadística de los colombianos, reafirmando su condición de líder como rector de las estadísticas en Colombia.
El Departamento Administrativo Nacional de Estadística, DANE, tendrá, además de las funciones que establece el artículo 59 de la Ley 489 de 1998, todas las consignadas en el Decreto 262 del 28 de enero de 2004.
La Estadística es la ciencia cuyo objetivo es reunir una información cuantitativa concerniente a individuos, grupos, series de hechos, etc. y deducir de ello gracias al análisis de estos datos unos significados precisos o unas previsiones para el futuro.
La estadística, en general, es la ciencia que trata de la recopilación, organización presentación, análisis e interpretación de datos numéricos con el fin de realizar una toma de decisión más efectiva.
En octubre de 1951 mediante el Decreto 2240, se separa la Oficina Nacional de Estadística de la Contraloría General de la República, es así como se crea la Dirección Nacional de Estadística, dependencia directa de la Presidencia de la República.
En el mes de octubre de 1953 bajo el gobierno del General Gustavo Rojas Pinilla, con amparo en el Decreto 2666, se crea el Departamento Administrativo Nacional de Estadística – DANE; posteriormente fue reorganizado en 1968 (Decreto 3167), siendo Presidente Carlos Lleras Restrepo; en diciembre de 1992, durante el gobierno de César Gaviria Trujillo, se llevó a cabo una re estructuración con base en el Decreto 2118. Mediante Decreto No.1174 del 29 de junio de 1999, bajo el gobierno de Andrés Pastrana, se adscribe al DANE el Instituto Geográfico Agustín Codazzi. Con el Decreto 1151 del 19 de junio de 2000, se adoptó una nueva estructura orgánica y posteriormente se realizaron los ajustes y modificaciones a la planta de personal, la cual fue adoptada mediante el Decreto 1187 del 28 de junio de 2000, en el gobierno de Andrés Pastrana Arango. Con el Decreto 263 del 28 de Enero de 2004 se modifica la planta de personal del Departamento Administrativo Nacional de Estadística y se dictan otras disposiciones. Con el Decreto 262 del 28 de Enero de 2004 se modifica la estructura del Departamento Administrativo Nacional de Estadística DANE y se dictan otras disposiciones.
c. Ramas de la estadística
La estadística descriptiva: que se dedica a los métodos de recolección, descripción, visualización y resumen de datos originados a partir de los fenómenos en estudio. Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de descriptores numéricos son la media y la desviación estándar. Resúmenes gráficos incluyen varios tipos de figuras y gráficos. La estadística descriptiva: es una ciencia que analiza series de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela, temperatura en los meses de verano, etc) y trata de extraer conclusiones sobre el comportamiento de estas variables.
• La inferencia estadística: que se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en cuestión teniendo en cuenta lo aleatorio e incertidumbre en las observaciones. Se usa para modelar patrones en los datos y extraer inferencias acerca de la población de estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas si/no (prueba de hipótesis), estimaciones de características numéricas (estimación), pronósticos de futuras observaciones, descripciones de asociación (correlación) o modelamiento de relaciones entre variables (análisis de regresión). Otras técnicas de modelamiento incluyen ANOVA, series de tiempo y minería de datos.
Ambas ramas (descriptiva e inferencial) comprenden la estadística aplicada. Hay también una disciplina llamada estadística matemática, la cual se refiere a las bases teóricas de la materia. La palabra estadísticas también se refiere al resultado de aplicar un algoritmo estadístico a un conjunto de datos, como en estadísticas económicas, estadísticas criminales, etc.
d. Tipos de variables.
Las variables pueden ser de dos tipos:
Variables cualitativas o atributos: no se pueden medir numéricamente (por ejemplo: nacionalidad, color de la piel, sexo).
Variables cuantitativas: tienen valor numérico (edad, precio de un producto, ingresos anuales).
Las variables también se pueden clasificar en:
Variables unidimensionales: sólo recogen información sobre una característica (por ejemplo: edad de los alumnos de una clase).
Variables bidimensionales: recogen información sobre dos características de la población (por ejemplo: edad y altura de los alumnos de una clase).
Variables pluridimensionales: recogen información sobre tres o más características (por ejemplo: edad, altura y peso de los alumnos de una clase).
Por su parte, las variables cuantitativas se pueden clasificar en discretas y continuas:
Discretas: sólo pueden tomar valores enteros (1, 2, 8, -4, etc.). Por ejemplo: número de hermanos (puede ser 1, 2, 3....,etc, pero, por ejemplo, nunca podrá ser 3,45).
Continuas: pueden tomar cualquier valor real dentro de un intervalo. Por ejemplo, la velocidad de un vehículo puede ser 80,3 km/h, 94,57 km/h...etc.
e. Definir individuo, población, muestra.
Individuo: cualquier elemento que porte información sobre el fenómeno que se estudia. Así, si estudiamos la altura de los niños de una clase, cada alumno es un individuo; si estudiamos el precio de la vivienda, cada vivienda es un individuo.
Población: conjunto de todos los individuos (personas, objetos, animales, etc.) que porten información sobre el fenómeno que se estudia. Por ejemplo, si estudiamos el precio de la vivienda en una ciudad, la población será el total de las viviendas de dicha ciudad.
Muestra: subconjunto que seleccionamos de la población. Así, si se estudia el precio de la vivienda de una ciudad, lo normal será no recoger información sobre todas las viviendas de la ciudad (sería una labor muy compleja), sino que se suele seleccionar un subgrupo (muestra) que se entienda que es suficientemente representativo.
f. Las fuentes de información.
Si el planteamiento del problema y de las hipótesis se acompaña del diseño y utilización de técnicas para obtener los datos que permiten probar esas hipótesis, se habla de Información Primaria; por Ejemplo, si se desea hacer el mismo estudio sobre la hipertensión con un registro directo de la tensión arterial en los pacientes o si se desea estudiar el nivel de ingresos de los colombianos en la última década y se recoge información mediante encuestas o entrevistas a un grupo de personas, se esta trabajando con información primaria.
Cuando el problema y las hipótesis se plantean en un momento posterior a la existencia de los datos, se habla de Información Secundaria, por ejemplo, cuando se quiere estudiar la hipertensión en un grupo de pacientes y se acude a las historias clínicas en el archivo del hospital o si se desea estudiar el nivel de ingresos de los colombianos en la última década utilizando los datos que posee el DANE, estamos utilizando información secundaria.
g. Las diferentes técnicas de recolección de información.
La Observación: Para que la observación sea considerada un instrumento de estudio o de una investigación científica se requiere que sirva a un problema previamente formulado, haya sido planeada con anterioridad, registrada sistemáticamente, relacionada con una teoría y sometida a prueba y control.
Toda observación debe responder a los siguientes interrogantes: ¿Qué debe ser observado? ¿Qué relación existe entre el observador y lo observado? ¿Qué observaciones deben registrarse? ¿Qué procedimientos serán usados para garantizar la seguridad de las observaciones?
La Entrevista: La entrevista es un reporte verbal de una persona que se realiza con el fin de obtener información primaria acerca de su conducta o acerca de las experiencias a las cuales ha estado expuesta. Se puede entender como conversación que sostienen dos personas con la finalidad específica de obtener alguna información importante para un estudio de carácter científico debe ser planeada y administrada cuidadosamente.
La Encuesta: Es un reporte escrito que revela a través de un cierto número de individuos a los cuales se le aplica, las relaciones generales entre las características de un gran número de variables, permite recolectar información con mayor cobertura y manejar más variables que en los casos de la observación y la entrevista.
Contrario a la entrevista, para el registro de la información, la encuesta no requiere de la presencia de otra persona, el mismo informante puede hacer el registro de la información completando por escrito un formulario previamente estructurado. Sin embargo en muchas ocasiones, buscando la mayor precisión en la información, se conviene en que una persona (encuestador) contacte el informante, le formule las preguntas y registre las respuestas. En estos casos la encuesta llega a confundirse con una entrevista estructurada.
La Ficha: Es un instrumento que reúne los elementos esenciales de un documento: Titulo, autor, editorial y fecha, así como un breve resumen de su contenido y su posible relación con el estudio o investigación para la cual se hace la consulta.
Es un medio de información que puede ser utilizado por el investigador o por otros investigadores. Su utilidad está en que permite consulta rápida.
Existen fichas bibliográficas y de contenido. Las primeras dedicadas a registrar la información básica sobre libros, artículos o periódicos y llevan número de ficha, lugar de investigación, titulo de la obra, editorial y fecha. Las fichas de contenido se dedican a registrar y consignar extractos o apartes completos, citas textuales, resúmenes de libros, ensayos, artículos y periódicos. Llevan número de ficha, área, tema, subtema, lugar de la investigación, titulo de la obra y fecha.
Ejemplo:
B. Una fábrica de chocolates va a sacar una chocolatina con un relleno nuevo. Para ello, decide hacer degustaciones de cuatro chocolatinas con rellenos diferentes en un supermercado y pide a las personas que escojan entre la chocolatina A,B, C o D.
La chocolatina A tiene relleno de fresa.
La chocolatina B tiene relleno de arequipe.
La chocolatina C tiene relleno de amareto.
La chocolatina D tiene relleno de maracuyá.
Los siguientes fueron los resultados de la degustación.
| B A C C D A B B C B |
| C B D D C B B C C D |
| A B C D A B B C D C |
| B C B B B D B B C A |
| B B C C D A B B A B |
| C B A C B C D A B C |
1. Determinar el número de personas que hizo la degustación.
| Valor numérico (Tipo de chocolatina) Xi | Frecuencia absoluta (# de personas) fi | Frecuencia relativa hi | Frecuencia relativa porcentual hi *100 |
| A | 9 | 9/60 = 0,15 | 9/60 *100 |
| B | 24 | 24/60 = 0,4 | 24/60 *100 |
| C | 18 | 18/60 = 0,3 | 18/60 *100 |
| D | 9 | 9/60 = 0,15 | 9/60 *100 |
| ∑ | n= 60 |
Frecuencia Absoluta (fi): frecuencia con la que aparece cada categoría de la variable. Nótese que la suma de las frecuencias absolutas es igual al número de observaciones
fi= n
Frecuencia relativa (hi): Cuando los datos son muchos es muy útil convertir las frecuencias en porcentajes o proporciones. En la terminología estadística la frecuencia relativa de un valor es la proporción de las observaciones que tiene ese valor. La frecuencia relativa se calcula dividiendo la frecuencia (número de incidencias) de ese valor entre el número total de observaciones.
fi =(frecuencia absoluta)/(total datos) = fi/n
3. Construir la tabla de frecuencias correspondiente a los datos.
3. Construir la tabla de frecuencias correspondiente a los datos.
Xi
|
fi
|
Frecuencia
relativa
|
Frecuencia
acumulada
|
|||
hi
|
hi*100
|
Fi
|
Hi
|
Hi*100
|
||
A
|
9
|
0,15
|
15
|
9
|
0.15
|
15
|
B
|
24
|
0,4
|
4.0
|
33
|
0.55
|
55
|
C
|
18
|
0,3
|
3.0
|
51
|
0.85
|
85
|
D
|
9
|
0,15
|
15
|
60
|
1.00
|
100
|
n= 60
|
||||||
4. Elaborar un diagrama de barras de los datos.
5. Construir el diagrama circular
fi
|
hi
|
Hi
|
Fi
|
Hi
|
|
A
|
9
|
0,15
|
15
|
9
|
0.2
|
B
|
24
|
0,4
|
40
|
33
|
0.6
|
C
|
18
|
0,3
|
30
|
51
|
0.9
|
D
|
9
|
0,15
|
15
|
60
|
1
|
n=60
|
100
|
C. El departamento médico de una universidad realiza el registro del peso de los estudiantes que hacen parte de los equipos que competirán en los juegos interuniversitarios.
A continuación, se presentan los datos aproximados a la libra más cercana de 50 estudiantes.
| 123 | 145 | 104 | 118 | 110 | 132 | 105 | 115 | 125 | 140 |
| 134 | 128 | 106 | 144 | 136 | 124 | 130 | 119 | 126 | 138 |
| 152 | 137 | 154 | 138 | 149 | 162 | 154 | 146 | 123 | 117 |
| 158 | 134 | 142 | 157 | 145 | 140 | 122 | 158 | 147 | 103 |
| 164 | 152 | 116 | 146 | 138 | 157 | 151 | 136 | 127 | 143 |
1. Agrupar los datos por intervalos
se ordena de menor a mayor
| 103 | 104 | 105 | 106 | 110 | 115 | 116 | 117 | 118 | 119 |
| 122 | 123 | 123 | 124 | 125 | 126 | 127 | 128 | 130 | 132 |
| 134 | 134 | 136 | 136 | 137 | 138 | 138 | 138 | 140 | 140 |
| 142 | 143 | 144 | 145 | 145 | 146 | 146 | 147 | 149 | 151 |
| 152 | 152 | 154 | 154 | 157 | 157 | 158 | 158 | 162 | 164 |
Número de intervalos: m=1+3.3 log(103)=8
Rango: r = 162-103= 61
Longitud del intervalo: A= r/m=61/8=8
Marca de clase: Mc = (102+110)/2=106
Intervalos
|
fi
|
hi
|
Fi
|
Hi
|
Mc
|
(102-110]
|
5
|
0.10
|
5
|
0.10
|
106
|
(111-119]
|
5
|
0.10
|
10
|
0.20
|
115
|
(120-128]
|
8
|
0.16
|
18
|
0.36
|
124
|
(129-137]
|
7
|
0.14
|
25
|
0.50
|
133
|
(138-146]
|
12
|
0.24
|
37
|
0.74
|
142
|
(147-155]
|
7
|
0.14
|
44
|
0.88
|
151
|
(156-164]
|
6
|
0.12
|
50
|
1.00
|
160
|
50
|
1
|
||||
2. interpretar: f1, h3, F3, H2, Mc3
f1 :significa que hay 5 estudiantes que pesan entre 102 y 110 libras.
h3: significa que el 0.16% de los estudiantes tienen peso entre 120 y 128 libras.
F3: 18 significa que hay 18 estudiantes que pesan entre 128 libras o menos.
H2: 0.20% significa que el 20% de los estudiantes estan pesando 119 libras o menos.
M3: 124 significa que el peso de 8 estudiantes esta en un promedio de 122 libras.
3. Realizar:
a. El histograma de frecuencias
Intervalos
|
fi
|
hi
|
Hi%
|
Fi
|
Hi
|
(102-110]
|
5
|
0.10
|
10
|
5
|
0.1
|
(111-119]
|
5
|
0.10
|
10
|
10
|
0.2
|
(120-128]
|
8
|
0.16
|
16
|
18
|
0.4
|
(129-137]
|
7
|
0.14
|
14
|
25
|
0.5
|
(138-146]
|
12
|
0.24
|
24
|
37
|
0.7
|
(147-155]
|
7
|
0.14
|
14
|
44
|
0.9
|
(156-164]
|
6
|
0.12
|
12
|
50
|
1
|
50
|
100
|
b. Diagrama Circular

c. El polígono de frecuencias
Intervalos
|
fi
|
Mc
|
(102-110]
|
5
|
106
|
(111-119]
|
5
|
115
|
(120-128]
|
8
|
124
|
(129-137]
|
7
|
133
|
(138-146]
|
12
|
142
|
(147-155]
|
7
|
151
|
(156-164]
|
6
|
160
|
d. La ojiva.
Intervalos
|
Fi
|
(102-110]
|
5
|
(111-119]
|
10
|
(120-128]
|
18
|
(129-137]
|
25
|
(138-146]
|
37
|
(147-155]
|
44
|
(156-164]
|
50
|
MEDIA
La media aritmética es el valor promedio de las muestras y es independiente de las amplitudes de los intervalos. Se simboliza como y se encuentra sólo para variables cuantitativas. Se encuentra sumando todos los valores y dividiendo por el número total de datos.
| 103 | 104 | 105 | 106 | 110 | 115 | 116 | 117 | 118 | 119 |
| 122 | 123 | 123 | 124 | 125 | 126 | 127 | 128 | 130 | 132 |
| 134 | 134 | 136 | 136 | 137 | 138 | 138 | 138 | 140 | 140 |
| 142 | 143 | 144 | 145 | 145 | 146 | 146 | 147 | 149 | 151 |
| 152 | 152 | 154 | 154 | 157 | 157 | 158 | 158 | 162 | 164 |
Intervalos
|
fi
|
Yi
|
fi Yi
|
(102-110]
|
5
|
106
|
530
|
(111-119]
|
5
|
115
|
575
|
(120-128]
|
8
|
124
|
992
|
(129-137]
|
7
|
133
|
931
|
(138-146]
|
12
|
142
|
1704
|
(147-155]
|
7
|
151
|
1057
|
(156-164]
|
6
|
160
|
960
|
50
|
6749
|
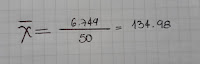
MEDIANA
La mediana de un conjunto de datos es el valor que cumple que la mitad de valores están por encima y la otra mitad por debajo. Así pues, para encontrarla basta con ordenar los elementos de menor a mayor y escoger el valor central.
Moda (Mo): Es el estadístico de tendencia central que identifica el dato con mayor frecuencia, es decir el que más se repite.
Cuando aparecen dos valores con frecuencias muy altas respecto a las demás se dice que la variable es bimodal e indica que la información proviene de dos poblaciones.
Cuando los datos están agrupados en intervalos de clase: primero se localiza el intervalo con mayor frecuencia absoluta el cual es llamado Intervalo Modal (lj) y la moda se obtiene a través de:
Intervalos
|
fi
|
hi
|
Fi
|
Hi
|
(102-110]
|
5
|
0.10
|
5
|
0.10
|
(111-119]
|
5
|
0.10
|
10
|
0.20
|
(120-128]
|
8
|
0.16
|
18
|
0.36
|
(129-137]
|
7
|
0.14
|
25
|
0.50
|
(138-146]
|
12
|
0.24
|
37
|
0.74
|
(147-155]
|
7
|
0.14
|
44
|
0.88
|
(156-
|
6
|
0.12
|
50
|
1.00
|
(164]
|
||||
50
|
| El intervalo modal es (111,119] con máxima frecuencia de 7 eje 129 D1=5 D2=1 y A=8
CUARTILES
Los cuartiles son valores que dividen una muestra de datos en cuatro partes iguales. Utilizando cuartiles puede evaluar rápidamente la dispersión y la tendencia central de un conjunto de datos, que son los pasos iniciales importantes para comprender sus datos.
| ||||||||||||||||||
Intervalos
|
fi
|
Fi
|
Hi
|
(102-110]
|
5
|
5
|
0.10
|
(111-119]
|
5
|
10
|
0.20
|
(120-128]
|
8
|
18
|
0.36
|
(129-137]
|
7
|
25
|
0.50
|
(138-146]
|
12
|
37
|
0.74
|
(147-155]
|
7
|
44
|
0.88
|
(156-164]
|
6
|
50
|
1.00
|
50
|
- El intervalo que acumula el 25% es (111,119]. y el anterior es (102,110], para el cálculo del primer cuartil, reemplazando los valores correspondientes se obtiene
Este valor indica que 15 estudiantes (el 25%) tienen un peso de 122 libras.
- El intervalo que acumula el 75% es (129,137] y el anterior es (120,128], con la información de la tabla se tiene:
ESTADÍSTICOS DE ESCALA
Rango y Rango intercuartílico:
Otro elemento importante para describir un conjunto de datos, es la variabilidad entendida como dispersión entre ellos.
Otro elemento importante para describir un conjunto de datos, es la variabilidad entendida como dispersión entre ellos.
Los estadísticos de variabilidad o de escala más utilizados son: El rango, el rango
intercuartílico, la varianza, la desviación estándar, el coeficiente de variación y la meda.
El rango: Es la diferencia entre el mayor y el menor de un conjunto de datos, esto es,
Rango = Xmax -Xmin
Donde Xmax representa el máximo Xmin representa el mínimo.
Rango intercuartilico: Para evitar la influencia de los valores extremos atípicos se pueden analizar solamente los valores intermedios del conjunto de datos ordenados. El rango intercuartílico es un indicador de la variabilidad que toma en cuenta solamente el 50% de los datos centrales de la distribución. Se calcula como la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1) así:
RIQ = Q3 – Q1
También como la diferencia entre los percentiles 75 y 25, es decir
RIQ = P75 – P25
Intervalos
|
fi
|
hi
|
Fi
|
Hi
|
(102-110]
|
5
|
0.10
|
5
|
0.1
|
(111-119]
|
5
|
0.10
|
10
|
0.2
|
(120-128]
|
8
|
0.16
|
18
|
0.4
|
(129-137]
|
7
|
0.14
|
25
|
0.5
|
(138-146]
|
12
|
0.24
|
37
|
0.7
|
(147-155]
|
7
|
0.14
|
44
|
0.9
|
(156-164]
|
6
|
0.12
|
50
|
1
|
50
|
||||
RIQ= Q3-Q1= 129-119=10
RANGO
R= Xmax - Xmin = 164-102= 62
Los resultados anteriores indican que la mitad de los datos ubicados en el centro de la distribución tiene una diferencia máxima de 10, mientras que la totalidad de los datos tiene una diferencia máxima de 62.
DESVIACIÓN MEDIA
COEFICIENTE DE VARIACIÓN




















No hay comentarios:
Publicar un comentario